[AI] 1. Regression

in Study on AI

[Deep Learning]을 정리하겠다.

Regression

Regression is 1) predicting the target y given a D-dimensional vector x 2) or estimating the relationship between x and y 3) or finding a function from x = (x1, x2, …, xp) to y

Linear Regression

Find the relationship(function) between two variables by fitting a linear equation to observed data

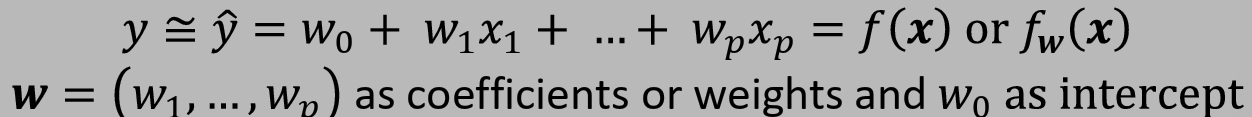
linear-regression

우리의 목표는 모든 x에 대해 실제값 y와 유사한 estimated y 또는 predicted y를 도출하는 것이다.

Loss Function, E

손실함수는 예측의 성능을 가리킨다. Regression의 목적은 결국 주어진 입력에 올바른 예측을 내놓는 것이기 때문에, 실제값과 예측값의 오차를 측정할 필요가 있다.

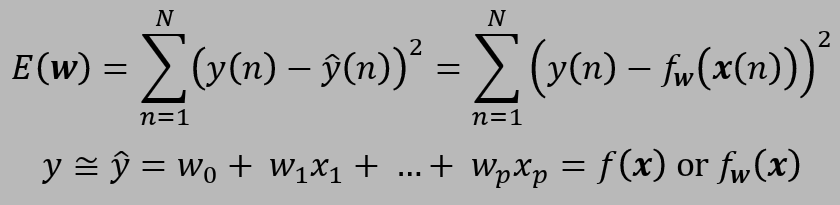
loss-function

Learning

학습은 파라미터(w)를 조정하면서 손실함수의 값을 감소시키는 과정이다.

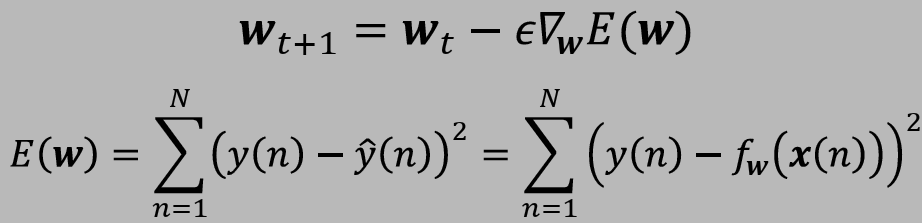
learning

  • gradient는 파라미터가 조정되야하는 방향을 제시한다.
  • learning rate은 weight가 조정되어야하는 정도를 결정한다.

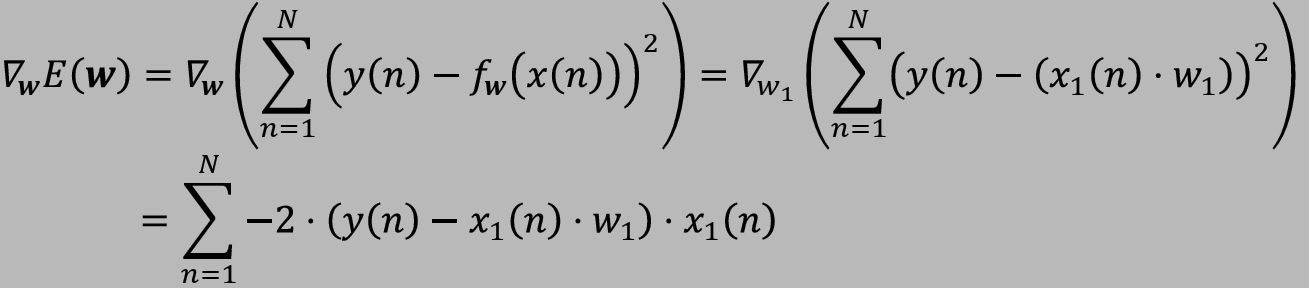
gradient

간단한 예제를 확인하고 싶다면 regression.ipynb를 참고하라.

Questions

Q1. Loss function이 실제값과 예측값의 차이의 총합인 것은 납득이 가고, 절댓값으로 표현하기 위해 제곱을 한 것도 알겠습니다. 그런데 절댓값을 하기 위해 굳이 제곱을 해야할 이유가 있나요? E값이 너무 크거나 작아질 것 같습니다.
A1. 1) 제곱을 통해 얻어지는 손실 함수는 연속적이고 미분 가능합니다. 이는 경사 하강법과 같은 최적화 알고리즘을 사용하여 손실을 최소화하는 파라미터를 찾는 데 도움이 됩니다. 또한 제곱 오차를 적분하는 것도 간단합니다. 2) 제곱을 통해 얻어지는 손실 함수는 이상치(특이치)의 영향을 완화시킵니다. 절대값 대신 제곱을 사용하면 이상치들의 오차에 비례하여 손실 함수의 값이 증가합니다. 이는 모델이 이상치에 민감하게 반응하지 않도록 도와줍니다.

Q2.
A2.